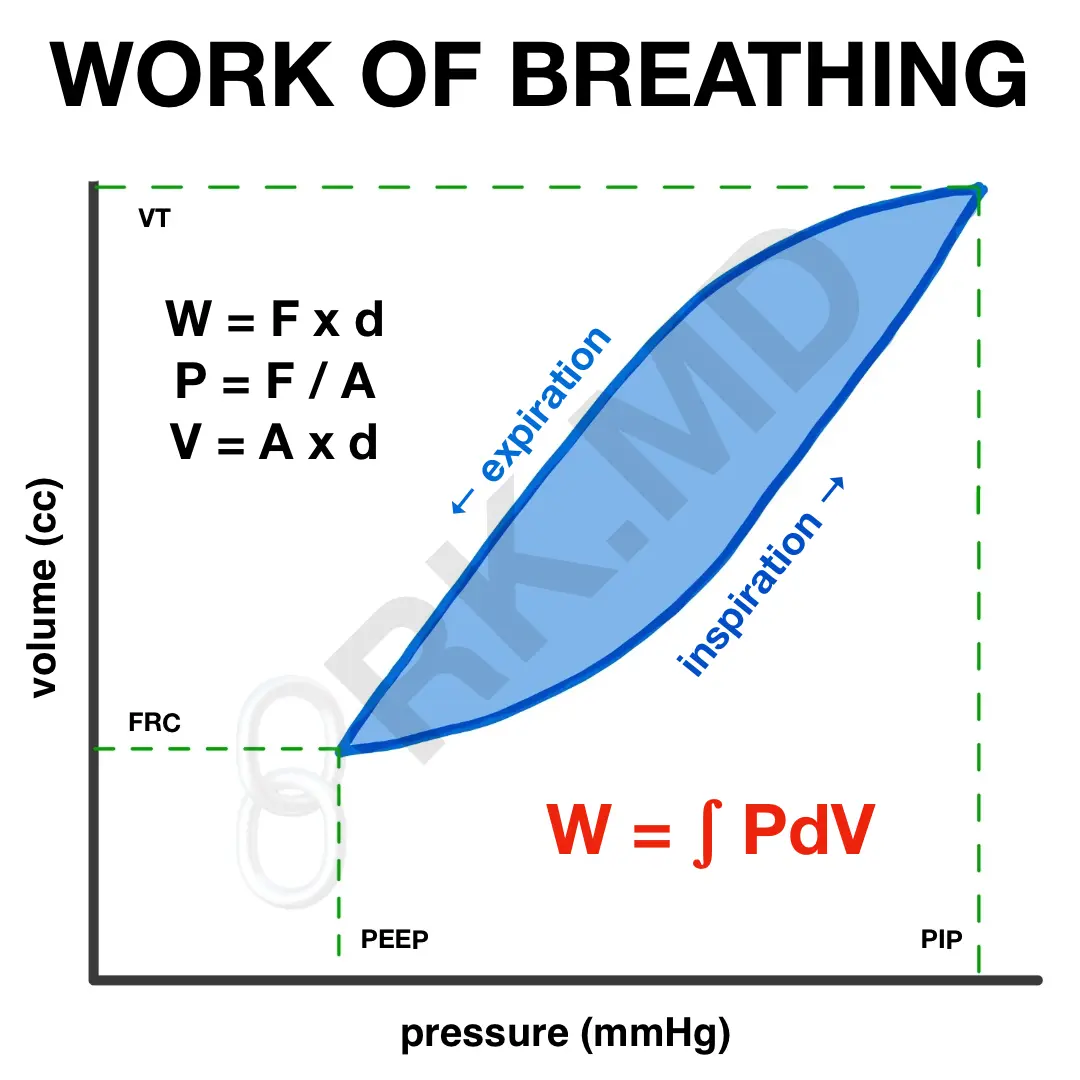
From a physics standpoint, work (W) = force (F) x distance (d). Similarly, pressure (P) = force (F) / area (A) and volume (V) = area (A) x distance (d). By rearranging these equations, one can show that:
work = pressure x volume
Pressure changes with volume based on a system’s compliance. In the pulmonary system, a highly compliant lung will be able to accommodate more volume with less pressure. A stiff lung (ARDS, high extravascular lung water, interstitial lung disease) will require much more pressure to drive in the same volume.
Knowing that inspiratory work will be equal to the integral (“area under the curve”) of PdV from the functional residual capacity (FRC, air left in the lung after normal expiration) to the tidal volume (VT, air inspired during normal breathing).
Calculus aside, how does this help us? Let’s take a case of cardiogenic pulmonary edema. This patient’s lung compliance will be poor due to extravascular lung water, interstitial edema, alveolar exudate, etc. Their pressure-volume loop would appear much flatter than illustrated suggesting that they require more pressure to achieve the same tidal volume as before, and as such, their work of breathing (the area under the curve) will be increased. By using adjuncts like bilevel positive airway pressure (BPAP), the work of breathing will be partly alleviated and their P-V loop will look more like this diagram.
Drop me a comment with questions! 🙂






Love the physics of it but a couple case scenarios would be most welcome to put this into practice.
Thanks Rishi